P-Value với Alpha
Trong CFA Level I, Quantitative Methods cũng là một nỗi sợ rất lớn đối với các bạn không có background về tính toán, số liệu. Có rất nhiều bạn học CFA nhầm lẫn giữa p-value, alpha (α) và kiểm định giả thuyết (hypothesis testing) và tiếp tục nhầm lẫn khi học CFA Level II.
Hãy cùng FTMS đọc thêm về dạng bài tập p-value, alpha (α) để hiểu được sự liên quan giữa các khái niệm này nhé:
Về bản chất, p-value và α cùng là một thứ: mức ý nghĩa (level of significance). Điểm khác nhau là, α được chọn trước, còn p-value thì do tính toán mà ra. Khi kiểm nghiệm một giả thuyết, chúng ta chọn một mức ý nghĩa (α), và sau đó tính toán số liệu thống kê dựa trên các dữ liệu để lấy được một mức ý nghĩa quan sát được (p-value). Cuối cùng, bạn so sánh 2 mức này (α và p-value) để đưa ra quyết định bác bỏ giả thuyết hoặc không bác bỏ giả thuyết.
α: Diện tích của miền bác bỏ (rejection region):
Theo định nghĩa, α là phần diện tích phía dưới phân phối chuẩn chuẩn hóa. Với kiểm nghiệm 1-đuôi (1-tailed test), α sẽ là toàn bộ phần diện tích ở phía đuôi phải (đối với right-tailed test) hoặc đuôi trái (đối với left-tailed test).
Đối với kiểm nghiệm 2-đuôi (2-tail test), phần diện tích sẽ được chia đều giữa phần đuôi phải và đuôi trái:
Vì p-value là mức ý nghĩa quan sát được, nó cũng là phần diện tích ở dưới phân phối chuẩn chuẩn hóa. Điểm khác biệt cốt lõi giữa α và p:
- α tương ứng với critical value (được chọn trước). Trong ví dụ ở trên, right-tailed test với critical value = 1.65; khi đó α tương ứng là 5% .
- p tương ứng to the calculated value (được tính toán ra): z-stat được tính từ các số liệu thống kê. Ví dụ, nếu ta tính ra z-stat = 1.80, giá trị p-value tương ứng sẽ là 3.59% (chúng ta có thể lấy được con số này bằng cách nhìn vào bảng phân phối chuẩn, giá trị ứng với z = 1.80 là 0.9641, đồng nghĩa với việc phần diện tích ở phía phải của z =1.80 là 1 − 0.9641 = 0.0359, hay 3.59%)
Nếu critical value = 1.65 và calculated value = 1.8, chúng ta sẽ bác bỏ giả thuyết null (null hypothesis). Một cách nói khác là nếu chúng ta có α = 5% và p-value = 3.59%, ta bác bỏ giả thuyết. Đồ thị minh họa như sau:
Tổng quát hóa: nếu p < α thì bác bỏ giả thuyết null, ngược lại nếu p > α thì không bác bỏ giả thuyết null.
Với kiểm nghiệm 1-đuôi, một vài ví dụ của p-value và giá trị z tương ứng là:
| 1-Tailed Test | |
| p-value | z-statistic |
| 0.50% | 2.58 |
| 1.00% | 2.33 |
| 1.50% | 2.17 |
| 2.00% | 2.05 |
| 2.50% | 1.96 |
| 5.00% | 1.64 |
| 10.00% | 1.28 |
| 15.00% | 1.04 |
| 20.00% | 0.84 |
Với kiểm nghiệm 2-đuôi, một vài ví dụ của p-value và giá trị z tương ứng là:
| 2-Tailed Test | |
| p-value | z-statistic |
| 0.50% | ±2.81 |
| 1.00% | ±2.58 |
| 1.50% | ±2.43 |
| 2.00% | ±2.33 |
| 2.50% | ±2.24 |
| 5.00% | ±1.96 |
| 10.00% | ±1.64 |
| 15.00% | ±1.44 |
| 20.00% | ±1.28 |
Lưu ý: Các giá trị bôi đỏ là các giá trị quan trọng nên ghi nhớ.
Ví dụ minh họa 1:
Bạn đang thực hiện kiểm nghiệm 2-đuôi. Mức ý nghĩa α được chọn là 5%. Bạn tính được p-value là 2%. Cho biết các mức critical value, z-statistic tương ứng ? Dựa vào đó, bác bỏ hay không bác bỏ giả thuyết null ?
Dựa vào quy tắc ở chung, p < α nên chúng ta bác bỏ giả thuyết null. Vùng bác bỏ (α – màu đỏ) và p-value – màu xanh được minh họa như sau:
Vì là kiểm định 2-đuôi, chúng ta tìm trong bảng các giá trị z tương ứng với 2.5% (= 5% / 2) và 1% (= 2% / 2). Ta tìm được critical value (z-crit) là 1.96 và −1.96 và z-stat là 2.33 hoặc -2.33. Do 1.96 < 2.33, và -1.96 > -2.33; ta bác bỏ giả thuyết null.
Ví dụ minh họa 2:
Bạn đang thực hiện kiểm nghiệm 1-đuôi với vùng bác bỏ nằm ở đuôi trái. Mức ý nghĩa α được chọn là 2.5%. Bạn tính được p-value là 4.5%. Cho biết các mức critical value, z-statistic tương ứng? Dựa vào đó, bác bỏ hay không bác bỏ giả thuyết null?
Dựa vào quy tắc ở trên, p > α nên chúng ta không bác bỏ giả thuyết null. Vùng bác bỏ (α – màu đỏ) và p-value – màu xanh được minh họa như sau:
Chúng ta thấy z-stat = -1.70, và z-crit = 1.96. Vì vậy không nằm trong vùng bác bỏ, và chúng ta không bác bỏ giả thuyết null.
Túm lại, bí quyết khi làm câu hỏi liên quan đến p-value và α là vẽ đồ thị của phân phối chuẩn giống như ở trên. Điều này sẽ giúp các bạn kiểm tra được luôn z-crit và z-stat các bạn tính ra có đúng hay không. Trải qua luyện tập, các bạn sẽ vẽ thành thục, và làm đúng 100% các câu hỏi này là chuyện quá đơn giản.
(Nguồn: tuihoctaichinh.com)
Có thể bạn sẽ thích
-
Chuẩn mực báo cáo tài chính quốc tế và những vấn đề đặt ra khi áp dụng tại Việt Nam
Nghiên cứu "Chuẩn mực báo cáo tài chính quốc tế và những vấn đề đặt ra khi áp dụng tại Việt Nam" do ThS Vũ Thị Diệp (Khoa Kế toán, Trường Đại học Kinh tế - Kỹ thuật Công nghiệp)
-
Bộ Tài Chính công bố 6 chuẩn mực kế toán công Việt Nam đợt 2
Ngày 06/07/2022, thừa ủy quyền Bộ trưởng Bộ Tài chính, Thứ trưởng Tạ Anh Tuấn đã ký ban hành Quyết định 1366/QĐ-BTC công bố 6 chuẩn mực kế toán công Việt Nam đợt 2.
-
Những thông tin về thực tập kế toán bạn cần biết
Thực tập kế toán là cơ hội giúp sinh viên kế toán, kiểm toán xây dựng kinh nghiệm cho bản thân trước khi ra trường. Cùng tìm hiểu nhé!
-
10 Thói quen hiệu quả của Giám đốc Tài chính (CFO)
Đây là 10 thói quen hiệu quả dành cho Giám đốc Tài chính được chia sẻ bởi Jack McCullough, Giám đốc Điều hành của Hội đồng Lãnh đạo CFO.
-
Quyết toán thuế TNCN và những thông tin bạn chưa biết
Quyết toán thuế TNCN là gì? Thời hạn nộp thuế trong bao lâu? Làm thế nào để có thể quyết toán thuế nhanh chóng, bài viết dưới đây sẽ hướng dẫn bạn nhé.
-
Tất tần tật về báo cáo tài chính của doanh nghiệp
Báo cáo tài chính là gì, quy định pháp luật về thuế, kế toán trong báo cáo tài chính ra sao? Cùng FTMS Việt Nam tìm hiểu trong bài viết này nhé!
-
7 Bí mật cho buổi thuyết trình báo cáo tài chính suôn sẻ
Chìa khóa then chốt để thành công trong buổi thuyết trình báo cáo tài chính là suy nghĩ thực tế khi trình bày báo cáo và thông tin tài chính.
-
5 mẹo tiết kiệm tối đa khi học ACCA
Nếu bạn đang theo học ACCA và xác định đây là mục tiêu quan trọng trong cuộc đời, đây là những mẹo giúp bạn tiết kiệm chi phí, thời gian
-
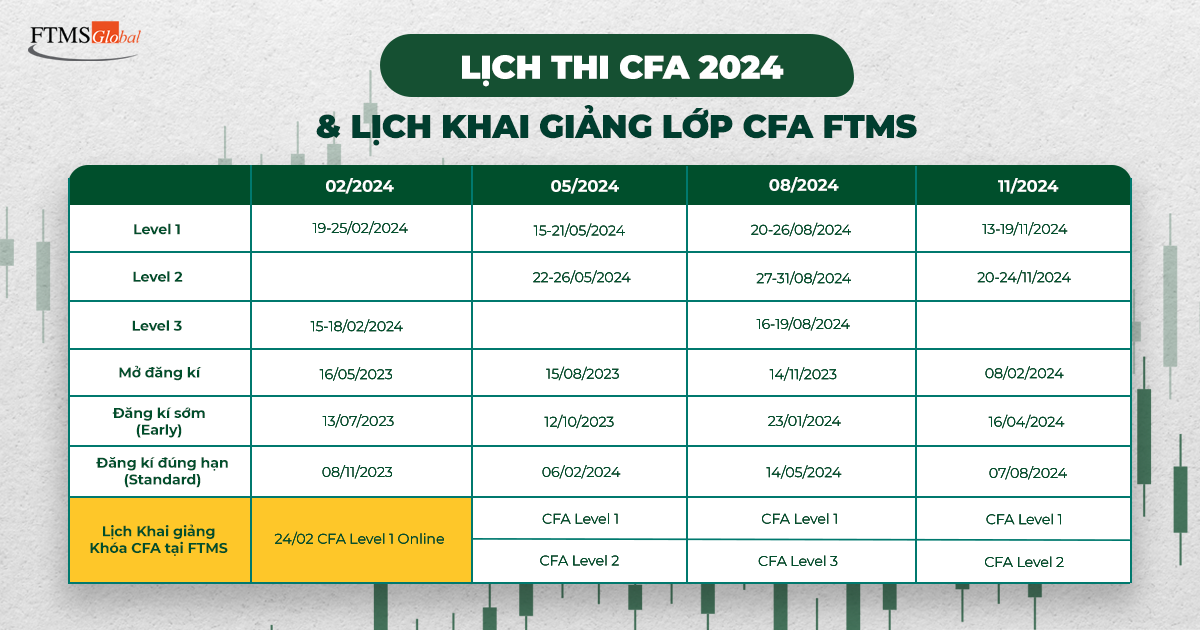
CẬP NHẬT LỊCH THI CFA 2024 VÀ LỊCH KHAI GIẢNG LỚP CFA FTMS
Note lại ngay lịch thi #CFA chính thức năm 2024 và thời hạn đăng ký thi để có cho mình kế hoạch chuẩn bị tốt nhất.
Bình luận